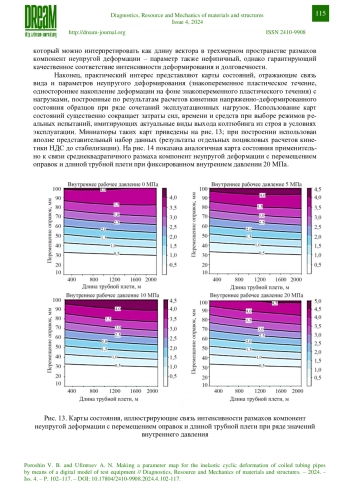
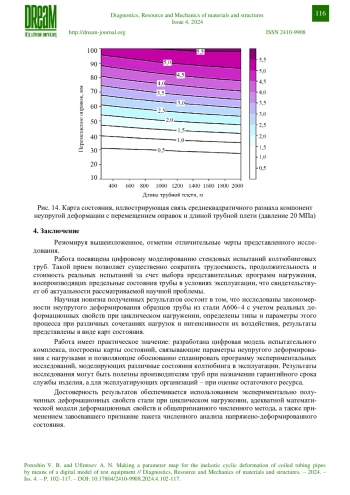
Методика ускоренных ресурсных испытаний применена к цифровому моделированию стендовых испытаний колтюбинговых труб. В пакете Ansys Mechanical сформированы конечно-элементные модели стенда и образца трубы. Расчетом кинетики напряженно-деформированного состояния образца получены петли неупругого гистерезиса для стабили-зированного цикла при ряде сочетаний эксплуатационных нагрузок: внутреннего давления, веса трубной плети, размера направляющего устройства. На этой основе построены карты состояний, связывающие параметры неупругого деформирования (знакопеременное пластическое течение, одностороннее накопление деформации на фоне знакопеременного пластического течения) с нагрузками. Использование карт состояний позволяет обоснованно спланировать программы реальных экспериментальных исследований для моделирования требуемого вида выхода колтюбинга из строя в условиях эксплуатации, что существенно сокращает временные, трудовые и материальные затраты.
Идентификаторы и классификаторы
Термин «колтюбинг» (coiled tubing) относится как к одной из прогрессивных технологий современного нефтегазового промысла, так и к ее основному объекту – длинной гибкой трубе, разматываемой с барабана и опускаемой в скважину на глубину до 1,5…2 км и более.
Список литературы
1. Кузнецов Н. Д., Цейтлин В. И. Эквивалентные испытания газотурбинных двигателей. – М. : Машиностроение, 1976. – 216 с.
2. Механические свойства сталей и сплавов при нестационарном нагружении : справочник. / Д. А. Гохфельд, Л. Б. Гецов, К. М. Кононов, Е. Т. Кульчихин, Ю. Н. Ребяков, О. С. Садаков, С. А. Тимашев, В. Н. Чепурский. – Екатеринбург : УрО РАН, 1996. – 408 c.
3. Experimental study on the influence of bending and straightening cycles for non-destructive and destructive coiled tubing / Y. Qian-Bei, S. Guohao, W. Gang, L. Jubao, Y. Ming, Z. Qiang // Engineer-ing Failure Analysis. – 2021. – No. 123. – P. 105218. – DOI: 10.1016/j.engfailanal.2021.105218.
4. Порошин В. Б., Буксбаум В. Б., Дружинин П. С. Методика прогнозирования долго-вечности колонны гибких труб на основе результатов лабораторных и стендовых испытаний // Вестник ЮУрГУ. Серия «Математика. Механика. Физика». – 2014. – Т. 6 (3). – С. 72–77.
5. Ильиных В. Н., Сызранцев В. Н. Построение математической модели для описания данных малоцикловых усталостных испытаний // Фундаментальная наука и технологии – перспективные разработки : материалы международной научно-практической конференции, Москва, 22–23 мая, 2013. – С. 224–226.
6. Порошин В. Б., Уфимцев А. Н. Цифровая модель испытательного стенда и МКЭ-анализ кинетики напряженно-деформированного состояния образцов колтюбинговых труб // Сборник научных статей Всероссийской научной конференции с международным участием, ЦИСП’2023 «Цифровая индустрия: состояние и перспективы развития–2023», Челябинск, 21–23 ноября 2023 г. – Челябинск : Издательский центр ЮУрГУ, 2024. – С. 377–386. – URL: http://omega.sp.susu.ru/glosic2023/articles/039.pdf
7. http: help/ans_elem/Hlp_E_SHELL181.html
8. Ramberg W., Osgood W.R. Description of stress–strain curves by three parameters. – NACA–TN–902, 1943. – 32 p.
Выпуск
Другие статьи выпуска
Использование искусственных нейронных сетей в металловедении для решения задач анализа изображений, в частности сегментации или классификации микроструктур металлов, включает в себя 6 основных этапов: определение проблемы, составление набора данных, выбор модели, обучение модели, оценка модели, интеграция с существующим рабочим процессом. В статье подробно рассмотрены эти этапы, приводится пример их реализации для се-мантической сегментации микроструктур композиционных покрытий, содержащих крупные первичные карбиды. Выделение карбидов нейронной сетью позволяет автоматизировать процесс определения их объемной доли в структуре покрытий.
В работе выполнено исследование процесса переноса тепла в пористой среде с внутренними источниками тепла. Рассматривается модельный материал – пористая пластина с топологией трижды периодических минимальных поверхностей, образованная элементарными ячейками типа Фишера – Коха S. В статье приведены результаты решения краевой за-дачи теплопроводности в тонкой пластине при симметричных граничных условиях первого рода. С использованием разработанного численно-аналитического метода получено простое по форме решение задачи с учетом топологических особенностей материала. При определении коэффициентов переноса и теплофизических свойств исследуемой области использованы методы вычислительной гомогенизации среды на основе CAE-моделирования в программном комплексе Ansys. В статье приведены графики распределения температуры в по-ристой пластине в различные моменты времени, выполнено сравнение полученных аналитических решений с численными. Результаты работы могут быть использованы при проектировании тепловой защиты тепловыделяющего оборудования, тепломассообменных трактов тепломеханического оборудования и др. Решения представлены в простом аналитическом виде, что делает возможным их использование широким кругом исследователей, инженеров и не требует использования дорогостоящего программного обеспечения и вычислительной техники.
Исследована структура, механические свойства и износостойкость композита, полученного методом самораспространяющегося высокотемпературного синтеза (СВС), со средним химическим составом, вес. %: 35,47 ± 1,5 Fe; 24,08 ± 1,4 Ti; 13,99 ± 0,5 Ni; 17,91 ± 0,4 B; 8,54 ± 0,5 C. В результате испытаний установлено, что композит обладает износостойкостью на уровне с одной из износостойких сталей Hardox 500. Композит характеризуется широким интервалом значений предела прочности на поперечный изгиб Rbm30 от 200 до 800 МПа. Сталь 40X показала предел прочности на изгиб Rbm30, равный 1590 МПа, а сталь Hardox 500 – 2970–3020 МПа. Композит имеет низкие значения ударной вязкости KCU = 0,02 МДж/м2 по сравнению со значениями KCU = 0,35 МДж/м2 для стали 40X и KCU = 1,59 МДж/м2 для стали Hardox 500. СВС-композит системы Fe–Ni–Ti–C–B не следует применять для деталей, работающих на изгиб и испытывающих ударные нагрузки, однако он отлично подойдет для защиты поверхностей деталей, подверженных интенсив-ному абразивному износу.
Сложные пористые структуры, основанные на трижды периодических минимальных поверхностях, обладающие высокими удельными показателями физико-механических характеристик, находят все более широкое применение во многих отраслях промышленности. Численный анализ имеет большое значение при оценке несущей способности и механического поведения таких структур. В работе представлены результаты конечно-элементного анализа напряженно-деформированного состояния структур, составленных из трижды пери-одических минимальных поверхностей, под действием сжимающей нагрузки. Сложность моделирования отклика таких структур на механическое воздействие заключается в большой размерности задачи, обусловленной необходимостью мелкой дискретизации, требуемой для адекватного представления сложной геометрии модели. Показаны этапы построения фасетной геометрии для формирования численных моделей. На примере поверхностей Шёна IWP и примитивов Шварца рассмотрено влияние типа и параметров данных структур на их меха-ническое поведение при сжатии. Выполнен анализ жесткостной эффективности в зависимо-сти от топологии структур.
Предложена и рассмотрена модель микромагнитного моделирования намагниченности ферримагнитной пленки, состоящей из сплава ферромагнитного и редкоземельного металлов. Показано, что модель качественно повторяет экспериментально наблюдаемые температурные зависимости намагниченности насыщения ферримагнитных сплавов для разного процентного содержания редкоземельного элемента, а также имеет аналогичную петлю магнитного гистерезиса. Результаты работы представляют интерес для теоретического анализа особенностей поведения намагниченности пленочных металлических наноструктур типа «ферримагнетик – тяжелый металл» и решения задач прикладного материаловедения и магнетизма.
В работе на основе анализа результатов теоретических и экспериментальных исследований сформулированы критерии, которым должны удовлетворять металлы для наблюдения в них туннелирования водорода, и методики измерения коэффициентов квантовой диффузии. Во-первых, должно быть достаточно малым (на уровне 0,15 нм) расстояние между ближайшими равновесными позициями атомов водорода в кристаллической решетке металла. Во-вторых, должна быть достаточно низкой температура Дебая металла, ниже 350 К. В-третьих, необходимым условием наблюдения туннелирования водорода является корректный выбор методики измерения коэффициентов диффузии водорода. Если в районе температуры Дебая коэффициент диффузии водорода по классическому механизму миграции находится на уровне 10−11 м2/с и выше, то целесообразно применять непрямые методики, основанные на эффекте Горского или измерении скорости спин-решеточной релаксации с помощью ядерного магнитного резонанса. При более низких значениях коэффициента классической диффузии в районе температуры Де-бая металла для наблюдения квантовой диффузии необходимо применять прямую методику ядерных реакций в режиме онлайн или ее же в сочетании с методом ядерных реакций.
С использованием критерия поврежденности выполнено исследование влияния напряженного состояния на деформационную способность алюмоматричного композита В95/10%SiC на примере обратного выдавливания типовой детали «стакан». Для оценки напряженно-деформированного состояния и поврежденности в процессе выдавливания вы-полнено моделирование процесса методом конечных элементов. Установлено, что для полу-чения качественного изделия необходимо осуществлять выдавливание в условиях всестороннего сжатия при околосолидусной температуре. Для экспериментальной проверки ре-зультатов моделирования спроектирован и изготовлен лабораторный штамп, особенностью которого является возможность регулирования величины сжимающих напряжений в процессе деформации. Получено бездефектное изделие при выдавливании. Установлено, что нагрев до околосолидусной температуры способствует разбиению первоначальной ячеистой струк-туры композита при внешнем нагружении.
Статистика статьи
Статистика просмотров за 2025 год.
Издательство
- Издательство
- ИМАШ УрО РАН
- Регион
- Россия, Екатеринбург
- Почтовый адрес
- 620049 г. Екатеринбург, ул.Комсомольская, 34
- Юр. адрес
- 620049 г. Екатеринбург, ул.Комсомольская, 34
- ФИО
- Швейкин Владимир Павлович (Директор)
- E-mail адрес
- ges@imach.uran.ru
- Контактный телефон
- +7 (343) 3744725