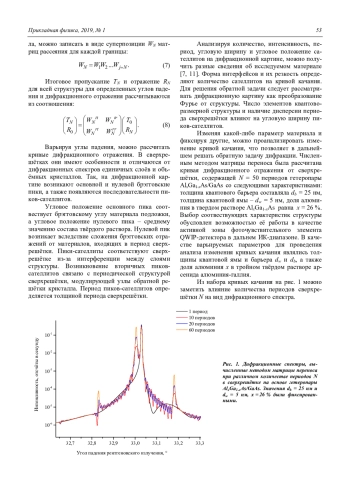
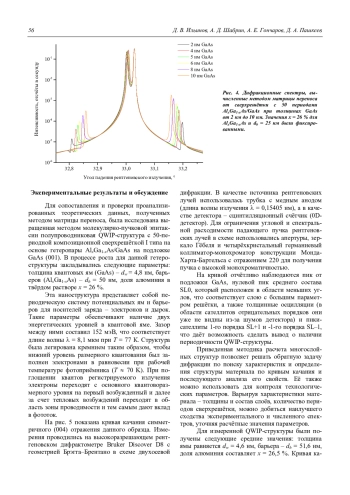
Изучены свойства спектров рентгеновского дифракционного отражения многослойных периодических гетероструктур AlGaAs/GaAs в зависимости от толщины и состава материала слоев и количества периодов. Показано, что количество и интенсивность дополнительных дифракционных максимумов на кривых качания возрастает с увеличением толщины слоев и количества периодов. Состав слоев не влияет на количество максимумов, а изменяет их угловое положение и полуширину. Проводилось сравнение численных расчетов с экспериментальными спектрами, измеренными для гетероструктуры, выращенной методом молекулярнопучковой эпитаксии и состоящей из 50 периодов, в которых барьер AlxGa1-xAs имел состав x 26,7 % и толщину d 51,6 нм, а квантовая яма GaAs – толщину d 4,6 нм. Установлено хорошее соответствие рассчитанных параметров с технологическими данными и результатами измерения на просвечивающем электронном микроскопе.
Properties of X-ray diffraction spectra of multilayer periodical heterostructures AlGaAs/GaAs have been studied in dependence of layers’ thickness and composition and the number of periods. It is shown that the number and intensity of additional diffraction maxima (satellites) on rocking curves increases together with increasing layers’ thickness and the number of periods. The composition of layers doesn’t affect the number of maxima but leads to changing their angular positions and the full width at half maximum values. Numerical calculations have been compared to experimental spectra observed on the heterostructure grown by means of molecular beam epitaxy consisting of 50 periods of AlxGa1-xAs with the composition x 26.7 % and the thickness d 51.6 nm and GaAs with the thickness d 4.6 nm. Good conformity between the calculated values and the technological parameters and experimental studies by means of transmission electron microscopy has been established.
Идентификаторы и классификаторы
- SCI
- Физика
- eLIBRARY ID
- 37027101
В работе на основе метода матрицы переноса построена численная модель для расчета дифракционных спектров многослойных полупроводниковых эпитаксиальных структур с применением динамической теории дифракции. Модель позволяет рассчитывать симметричные и асимметричные кривые качания различных типов сканирования с высокой точностью. Из сравнения расчетной кривой качания с экспериментальной для QWIPструктуры на основе гетеропары AlxGa1-xAs/GaAs можно сделать вывод о корректности численной модели.
Из проведённого анализа результатов моделирования дифракционных спектров сверхрешё- ток на основе гетеропары AlxGa1-xAs/GaAs (интенсивность и угловые положения пиков, количество пиков-сателлитов и толщинных осцилляций) при различных технологических параметрах показано, что:
– толщины квантовых ям и барьеров определяют относительную интенсивность нулевого и основного пиков; положение пиков-сателлитов отрицательного и положительного порядков смещается к нулевому и основному пикам соответственно с ростом толщины периода сверхрешётки;
– доля алюминия в твёрдом растворе AlxGa1-xAs не влияет на количество пиковсателлитов на кривой качания, меняя лишь их угловое положение и полуширину вследствие изменения постоянной кристаллической решётки в структуре;
– количество толщинных осцилляций растёт с увеличением количества периодов сверхрешётки, а их амплитуда падает.
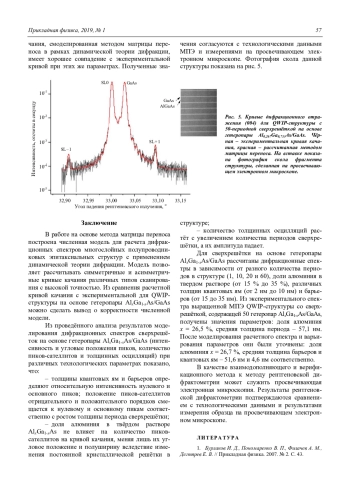
Для сверхрешётки на основе гетеропары AlxGa1-xAs/GaAs рассчитаны дифракционные спектры в зависимости от разного количества периодов в структуре (1, 10, 20 и 60), доли алюминия в твердом растворе (от 15 % до 35 %), различных толщин квантовых ям (от 2 нм до 10 нм) и барьеров (от 15 до 35 нм). Из экспериментального спектра выращенной МПЭ QWIP-структуры со сверхрешёткой, содержащей 50 гетеропар AlxGa1-xAs/GaAs, получены значения параметров: доля алюминия x = 26,5 %, средняя толщина периода – 57,1 нм. После моделирования расчетного спектра и варьирования параметров они были уточнены: доля алюминия x = 26,7 %, средняя толщина барьеров и квантовых ям – 51,6 нм и 4,6 нм соответственно.
В качестве взаимодополняющего и верификационного метода к методу рентгеновской дифрактометрии может служить просвечивающая электронная микроскопия. Результаты рентгеновской дифрактометрии подтверждаются сравнением с технологическими данными и результатами измерения образца на просвечивающем электронном микроскопе.
Список литературы
1. Бурлаков И. Д., Пономаренко В. П., Филачев А. М., Дегтярев Е. В. // Прикладная физика. 2007. № 2. С. 43.
Д. В. Ильинов, А. Д. Шабрин, А. Е. Гончаров, Д. А. Пашкеев 58
2. Rogalski A. // Progress in Quantum Electronics. 2003. Vol. 27. No. 2. P. 59.
3. Бурлаков И. Д., Болтарь К. О., Власов П. В., Лопухин А. А., Торопов А. И., Журавлев К. С., Фадеев В. В. // Прикладная физика. 2016. № 3. С. 58.
4. Rogalski A., Martyniuk P., Kopytko M. // Applied Physics Reviews. 2017. Vol. 4. P. 031304.
5. Benyahia D., Kubiszyn L., Michalczewski K., Bogulski J., Keblowski A., Martyniuk P., Piotrowski J., Rogalski A. // Nanoscale Research Letters. 2018. Vol. 13. P. 196.
6. Rogalski A., Kopytko M., Martyniuk P. // Proceedings of SPIE. 2017. Vol. 13. P. 10177.
7. Шабрин А. Д., Гончаров А. Е., Пашкеев Д. А., Ляликов А. В., Егоров А. В. // Прикладная физика. 2017. № 3. С. 101.
8. Нестерец Я. И., Пунегов В. И., Павлов К. М. // Журнал технической физики. 1999. Т. 69. № 2. С. 44.
9. Reyner C. J., Kiefer A. M., Ariyawansa G., Duran J. M., Scheihing J. E. // Crystals. 2016. Vol. 6. P. 150.
10. Старкова М. В., Лихушина Е. В., Свешников С. В., Кацнельсон А. А. // Вестник МГУ. Физика и Астрономия. 1999. № 6. С. 38.
11. Маслова О. А., Захарченко И. Н., Бунина О. А., Юзюк Ю. И., Ortega N., Kumar A., Katiyar R. S. // Физика твердого тела. 2012. Т. 54. № 8. С. 1526.
12. Kladko V. P., Datsenko L. I., Korchovyi A. A., Machulin V. F., Lytvyn P. M., Shalimov A. V., Kuchuk A. V., Kogutyuk P. P. // Semiconductor Physics, Quantum Electronics & Optoelectronics. 2003. Vol. 6. No. 3. P. 392.
1. I. D. Burlakov, V. P. Ponomarenko, А. M. Filachev, and E. V. Degtyarev, Prikl. Fiz., No. 2, 43 (2007).
2. A. Rogalski, Progress in Quantum Electronics 27 (2), 59 (2003).
3. I. D. Burlakov, K. O. Boltar, P. V. Vlasov, A. A. Lopukhin, A. I. Toropov, K. S. Juravlev, and V. V. Fadeev, Prikl. Fiz., No. 3, 58 (2016).
4. A. Rogalski, P. Martyniuk, and M. Kopytko, Applied Physics Reviews 4, 031304 (2017).
5. D. Benyahia, L. Kubiszyn, K. Michalczewski, J. Bogulski, A. Keblowski, P. Martyniuk, J. Piotrowski, and A. Rogalski, Nanoscale Research Letters, 13, 196 (2018).
6. A. Rogalski, M. Kopytko, and P. Martyniuk, Proceedings of SPIE 13, 10177 (2017).
7. A. D. Shabrin, A. E. Goncharov, D. A. Pashkeev, A. V. Lyalikov, and A. V. Egorov, Journal of Communications Technology and Electronics 63 (3), 309 (2018).
8. Ya. I. Nesterec, V. I. Punegov, and K. M. Pavlov, Tech. Phys. 69 (2), 44 (1999).
9. C. J. Reyner, A. M. Kiefer, G. Ariyawansa, J. M. Duran, and J. E. Scheihing, Crystals 6, 150 (2016).
10. M. V. Starkova, E. V. Lihushina, S. V. Sveshnikova, and A. A. Kacnelson, Vestnik MGU, Fizika i Astronomiya, No. 6, 38 (1999).
11. O. A. Maslova, I. N. Zaharchenko, O. A. Bunina, U. I. Uzuk, N. Ortega, A. Kumar, and R. S. Katiyar, Phys. Solid State 54 (8), 1526 (2012).
12. V. P. Kladko, L. I. Datsenko, A. A. Korchovyi, V. F. Machulin, P. M. Lytvyn, A. V. Shalimov, A. V. Kuchuk, and P. P. Kogutyuk, Semiconductor Physics, Quantum Electronics & Optoelectronics 6 (3), 392 (2003).
Выпуск

С О Д Е Р Ж А Н И Е
ОБЩАЯ ФИЗИКА
Свешников В. М., Третьяков А. С. Численно-аналитические алгоритмы интегриро-вания уравнений движения заряженных частиц в электрических полях 5
ФИЗИКА ПЛАЗМЫ И ПЛАЗМЕННЫЕ МЕТОДЫ
Лебедев Ю. А. 10-й Международный научный семинар по СВЧ-разрядам – X-th International Workshop on Micro-wave Discharges: Fundamentals and Applications (MD-10) 11
Скалыга В. А., Голубев С. В., Изотов И. В., Лапин Р. Л., Разин С. В., Сидоров А. В., Шапошников Р. А. Сильноточные импульсные ЭЦР-источники ионов 17
Ахметов М. Н., Ахметов Н. Д., Гимадеев М. М., Кривошеев В. А. Метод расчёта формирования и движения фронта ударной волны в высоковольтном электрическом разряде в воде 25
Золотухин Д. Б., Бурдовицин В. А., Окс Е. М., Панченко Н. А. Потенциал составной металлической мишени при её облучении электронным пучком в форвакуум-ной области давлений 30
Кравченко Д. А., Ловцов А. С. Влияние траекторий первичных электронов на эффективность работы газоразрядной камеры ионного двигателя 35 Балданов Б. Б., Ранжуров Ц. В., Сордонова М. Н., Будажапов Л. В. Влияние плазменной модификации поверхности семян зерновых культур на их посевные свойства 41
ФОТОЭЛЕКТРОНИКА
Войцеховский А. В., Кульчицкий Н. А., Несмелов С. Н., Дзядух С. М., Варавин В. С., Дворец-кий С. А., Михайлов Н. Н., Якушев М. В., Сидоров Ю. Г. Воздействие оптического излучения на адмиттанс МДП-структур на основе МЛЭ n-Hg0,78Cd0,22Te с приповерхностными варизонными слоями 46
Ильинов Д. В., Шабрин А. Д., Гончаров А. Е., Пашкеев Д. А. Численный анализ спектров рентгеновского дифракционного отражения от сверхрешеток на основе гетеропары AlGaAs/GaAs в зависимости от структурных параметров 51 Жегалов С. И. Модель нейронной схемы формирования изображения для ФПУ с микросканированием 59
ФИЗИЧЕСКОЕ МАТЕРИАЛОВЕДЕНИЕ
Буркова Л. А., Иванов Д. К., Иванов К. Г., Щербаков А. П. Осцилляции напряжения в тонких углеродных пленках в области отрицательного дифферен-циального сопротивления 66
Зау Йе Мьинт, Кхин Маунг Хтау, Хтет Вэй Ян Чжо, Хтет Ко Ко Зау, Васильева Т. М. Модификация тонких пленок хитозана в электронно-пучковой плазме 71
Ципинова А. Х., Шериева Э. Х., Азизов И. К. Деформационный отклик плоских микрокристаллов галогенида серебра AgBr на излучение видимого спектра 77
Вашуков Ю. А., Демичев С. Ф., Еленев В. Д., Малинский Т. В., Миколуцкий С. И., Хомич Ю. В., Ямщиков В. А. Лазерная обработка поверхности металлических сплавов для диффузионной сварки 82
Зиенко С. И., Слабковский Д. С. Определение происхождения ограненных алмазов с помощью интегральной функции рас-пределения спектров люминесценции 88
ФИЗИЧЕСКАЯ АППАРАТУРА И ЕЁ ЭЛЕМЕНТЫ
Булярский С. В., Гусаров Г. Г., Лакалин А. В., Матына Л. И., Олейник С. П. Экранирование электрического поля углеродных нанотрубок или наностержней из оксида цинка вследствии их взаимного влияния 93
ИНФОРМАЦИЯ
Правила для авторов 98
C O N T E N T S
GENERAL PHYSICS
V. M. Sveshnikov and A. S. Tretyakov Numerical-analytical algorithms for integrating the equations of motion of charged particles in electric fields 5
PLASMA PHYSICS AND PLASMA METHODS
Yu. A. Lebedev Xth International Workshop on Microwave Discharges: Fundamentals and Applications (MD-10) 11
V. A. Skalyga, S. V. Golubev, I. V. Izotov, R. L. Lapin, S. V. Razin, A. V. Sidorov, and R. A. Shaposhnikov High-current pulsed ECR ion sources 17
M. N. Akhmetov, N. D. Akhmetov, M. M. Gimadeev, and V. A. Krivosheev Method of calculating shock wave front generation and motion on a high voltage electric discharge in water 25
D. B. Zolotukhin, V. A. Burdovitsin, E. M. Oks, and N. A. Panchenko Potential of an isolated complex target during its irradiation by an electron beam in the forevacuum pressure range 30
D. A. Kravchenko and A. S. Lovtsov Primary electrons trajectories influence on performance efficiency of ion thruster discharge cham-ber 35
B. B. Baldanov, Ts. V. Ranzhurov, M. N. Sordonova, and L. V. Budazhapov Effect of plasma surface modification of seeds on the sowing properties of agricultural crops 41
PHOTOELECTRONICS
A. V. Voitsekhovskii, N. A. Kulchitsky, S. N. Nesmelov, S. M. Dzyadukh, V. S. Varavin, S. A. Dvo-retsky, N. N. Mikhailov, M. V. Yakushev, and G. Yu. Sidorov The effect of optical radiation on the admittance of MIS structures based on MBE n-Hg0.78Cd0.22Te with near-surface graded-gap layers 46
D. V. Ilinov, A. D. Shabrin, A. E. Goncharov, and D. A. Pashkeev Numerical analysis of the X-ray diffraction spectra of AlGaAs/GaAs superlattices in relation to structural parameters 51
S. I. Zhegalov Model of a neural image formation scheme for the FPA with microscanning 59
PHYSICAL SCIENCE OF MATERIALS
L. A. Burkova, D. K. Ivanov, K. G. Ivanov, and A. P. Shcherbakov Voltage oscillations in thin carbon films in the region of negative differential resistance 66
Zaw Ye Myint, Khin Maung Htay, Htet Wai Yan Kyaw, Htet Ko Ko Zaw, and T. M. Vasilieva Modification of thin chitosan films by means of electron-beam plasma 71
A. Kh. Tsipinova, E. Kh. Sherieva, and I. K. Azizov Deformation response of a flat AgBr microcrystals on the visible radiation 77
Yu. A. Vashukov, S. F. Demichev, V. D. Elenev, T. V. Malinskiy, S. I. Mikolutskiy, Yu. V. Khomich, and V. A. Yamshchikov Laser processing of metal alloys for diffusion welding 82
S. I. Zienko and D. S. Slabrovsky Determination of origin of deteriated diamonds by the integral function of distribution of lumines-cence spectra 88
PHYSICAL APPARATUS AND ITS ELEMENTS
S. V. Bulyarskiy, G. G. Gusarov, A. V. Lakalin, L. I. Matyna, and S. P. Oleynik Shielding of the electric field of carbon nanotubes or zinc oxide nanorods due to their mutual in-fluence 93
INFORMATION
Rules for authors 98
Другие статьи выпуска
Целью данной работы является сравнение экранирования электрического поля у концов холодных эмиттеров на основе углеродных нанотрубок (УНТ) и наностержней оксида цинка. Были выполнены расчеты напряженности электрического поля одиночного эмиттера, и эмиттера, расположенного в центре массива из 25 одинаковых элементов. Согласно проведенным расчетам, коэффициент усиления поля у концов нанообъектов по сравнению с его средним значением для случая одиночных УНТ в 4 раза больше, чем для одиночных наностержней ZnO. В случае массива нанообъектов коэффициент усиления у конца нанотрубки лишь в 1,5 раза превышает значение такового у конца наностержня, что является результатом экранирующего влияния окружения. При сопоставимости работ выхода из углеродных нанотрубок и наностержней ZnO следует ожидать близких значений плотностей токов эмиссии катодов рассматриваемых нанообъектов. Однако, в силу геометрии, условия тепло-отвода для случая наностержней оксида цинка предпочтительней. Следствием этого может быть большая временная стабильность холодных катодов на основе наностержней оксида цинка.
Установлено, что интегральные функции распределения спектров люминесценции ограненных алмазов природного происхождения по форме и положению в частотной области заметно отличаются от образцов бриллиантов лабораторного изготовления. Данные интегральные функции могут использоваться для идентификации бриллиантов различного происхождения.
При обработке поверхности CuCrZr-бронзы сканирующим пучком наносекундных лазерных импульсов с длиной волны излучения 355 нм выявлено образование структур в виде сфер диаметром около 500 нм, расположенных на ножках высотой до 1 мкм. Обнаружено влияние плотности энергии лазерного излучения и скорости сканирования лазерным пучком на формирование данных субмикронных структур. Показана возможность улучшения качества соединения металлических сплавов при диффузионной сварке за счет лазерной обработки поверхностей заготовок.
В работе рассматривается деформационное действие света на крупные плоские микрокристаллы (ПМК) галогенидов серебра AgBr толщиной порядка 40–80 нм и диаметром в пределах 40–500 мкм, синтезированных методом контролируемой двухструйной эмульсификации (КДЭ).
Экспериментально исследована возможность модификации тонких пленок хитозана в электронно-пучковой плазме кислорода. Плазмохимическая модификация пленок приводила к снижению кристалличности, увеличению содержания кислородсодержащих полярных групп, в первую очередь, –СООН. Также наблюдалось, по сравнению с исходными образцами, повышение гидрофильности поверхности хитозановых пленок, модифицированных в электроннопучковой плазме, причем этот эффект сохранялся по крайней мере в течение трех недель после обработки.
Исследована тонкая пленка, полученная осаждением на подложку фрагментов углеродного волокна, образовавшихся вследствие его взрывного разрушения при пропускании сильных импульсных токов. Показано, что при напряжении порядка 300 В пленка входит в область отрицательного дифференциального сопротивления N-типа, в которой наблюдаются релаксационные осцилляции напряжения. Предложен механизм возникновения отрицательного дифференциального сопротивления и появления осцилляций напряжения.
Статья является развитием градиентного подхода с нейронной схемой в качестве формирователя изображения для ФПУ с микросканированием. В рассматриваемой модели широко используется метод наименьших квадратов (МНК). Данная МНК-модель обеспечивает оценку вариантов обработки на основе сопоставления градиентов сигналов и матриц неизвестных, соответствующих формируемым изображениям. Модель включает сопоставление градиентов сигналов и неизвестных, систему линейных уравнений относительно неизвестных, соответствующую системе нейронную схему; традиционное решение системы используется для формирования критерия остановки нейронной схемы.
Проведены исследования влияния оптического излучения на адмиттанс МДП-структур на основе n(p)-Hg1–xCdxTe (x = 0,21–0,23), выращенного методом молекулярно-лучевой эпитаксии с приповерхностными варизонными слоями с повышенным содержанием CdTe и без таких слоев. Установлено, что освещение существенно изменяет вид полевых зависимостей емкости и приведенной проводимости в режиме инверсии для структуры с варизонным слоем. Изменение емкости МДП-структуры в режиме инверсии происходит по двум механизмам: уменьшение времени формирования инверсионного слоя, увеличение значения емкости в минимуме низкочастотной ВФХ. Приведенная проводимость МДП-структуры при освещении уменьшается на низких частотах, но возрастает на высоких частотах.
Изучено изменение поверхностных свойств семян пшеницы под воздействием нетермической плазмы, инициируемой тлеющим разрядом атмосферного давления в аргоне. Воздействие на оболочку семени неравновесной плазмы тлеющего разряда атмосферного давления приводит к модификации поверхности семени, заключающееся в проявлении на поверхности семени мелкоячеистой сетчатой структуры. При увеличении длительности воздействия или мощности разряда эффекты травления на поверхности семени усиливаются, но при этом скорость прорастания семян не увеличивается с интенсификацией параметров обработки.
В данной работе приводятся результаты моделирования плазмы в газоразрядной камере ион-ного двигателя ИД-50. Для получения этих данных использовалась двухмерная кинетическая модель, основанная на методе «частиц в ячейках» (Particle-in-Cell). Анализ результатов, которые лежат в хорошем соответствии с экспериментальными данными, позволил выявить корреляцию между траекториями первичных электронов и эффективностью работы газоразрядной камеры. Показана взаимосвязь между геометрией магнитной системы, определяющей траектории первичных электронов, картиной течения ионной компоненты и величиной энергетической цены иона.
В статье представлены результаты измерения потенциала изолированного коллектора, облучаемого электронным пучком в среднем вакууме, при различных значениях – коэффициента вторичной электронной эмиссии электронов (ВЭЭ). Изменение обеспечено плавным перемещением относительно электронного пучка коллектора, составленного из двух металлов (алюминия и титана) с резко различающимися значениями коэффициента ВЭЭ. Предложена модель, удовлетворительно описывающая измеренную зависимость, и методика, позволяющая по установившемуся потенциалу изолированного коллектора оценивать коэффициент ВЭЭ различных материалов, в том числе и диэлектриков.
статье представлены результаты экспериментального исследования процесса формирования и движения ударных волн при высоковольтном электрическом разряде в воде. Для рассматриваемого режима разрядов определены давление и скорость фронта ударной волны и рассчитан момент достижения ударной волной максимальной интенсивности.
В настоящее время в ряде ионных электронно-циклотронных резонансных (ЭЦР) источников для создания и нагрева плазмы используется мощное микроволновое излучение современных гиротронов. Вследствие большой мощности излучения такие системы работают в основном в импульсном режиме. Этот тип ионных ЭЦР-источников был разработан в Институте прикладной физики Российской академии наук, и большая часть экспериментальных исследований была выполнена на установке SMIS 37. Для создания плазмы на SMIS 37 использовались гиротроны с частотами 37,5 и 75 ГГц и максимальными мощностями 100 и 200 кВт, соответственно. Такое микроволновое излучение позволяло создавать плазму с уникальными параметрами: электронной плотностью более 1013 см–3, электронной температурой 50–300 эВ, ионной температурой около 1 эВ. Принципиальное отличие этих систем от традиционных ЭЦР-источников состоит в реализации так называемого квазигазодинамического режима удержания плазмы в ловушке. В соответствии с режимом удержания такие источники были названы «газодинамическими ЭЦР-источниками». В этих системах время жизни плазмы обычно составляет несколько десятков микросекунд, что в сочетании с высокой электронной концентрацией приводит к формированию плазменных потоков из ловушки с плотностями до 1–10 А/см2. Была продемонстрирована возможность создания пучков МЗИ (азот, аргон) и протонных (дейтронных) пучков с токами на уровне сотен мА при среднеквадратичном нормализованном эмиттансе порядка 0,1 ×мм×мрад. Следующим шагом в исследованиях является переход к непрерывному режиму работы газодинамического ионного ЭЦР-источника (ЭЦР ИИ). С этой целью в ИПФ РАН создаётся новая экспериментальная установка. Для получения плазмы в будущем источнике будет использоваться излучение гиротронов на частотах 28 и 37,5 ГГц. В настоящей работе дан обзор полученных результатов и состояния дел по монтажу нового источника.
Дан обзор новых интересных результатов, представленных на 10-м Международном научном семинаре по СВЧ-разрядам (X-th International Workshop on Microwave Discharges: Fundamentals and Applications) состоявшемся с 3 по 7 сентября 2018 года в г. Звенигороде Московской области.
Предложены и экспериментально исследованы численно-аналитические алгоритмы интегрирования уравнений движения заряженных частиц в электрических полях. Необходимость в разработке таких алгоритмов возникла при моделировании интенсивных пучков заряженных частиц в протяженных системах. Характерной задачей при этом является по возможности точное определение расширения пучка и его угловой расходимости на значительном расстоянии от поверхности старта (эмиттера). Применение классических численных алгоритмов не давало адекватных результатов. Поэтому возникло предложение на каждом шаге численного интегрирования использовать аналитическое решение уравнений движения, сделав упрощающие предположения об электрических полях. Упрощающие предположения в пределах шага численного интегрирования, дающие достаточную точность и, в то же время, несложное решение, состояли в следующем: в продольном направлении поле предполагается постоянным, а в поперечном – линейным по координате, что характерно для интенсивных пучков. Дано экспериментальное сравнение численно-аналитических алгоритмов с численными алгоритмами, которое показало преимущество разработанного подхода.
Статистика статьи
Статистика просмотров за 2025 - 2026 год.
Издательство
- Издательство
- АО "НПО "ОРИОН"
- Регион
- Россия, Москва
- Почтовый адрес
- 111538, г Москва, р-н Вешняки, ул Косинская, д 9
- Юр. адрес
- 111538, г Москва, р-н Вешняки, ул Косинская, д 9
- ФИО
- Старцев Вадим Валерьевич (ГЕНЕРАЛЬНЫЙ ДИРЕКТОР)
- E-mail адрес
- orion@orion-ir.ru
- Контактный телефон
- +7 (499) 3749400