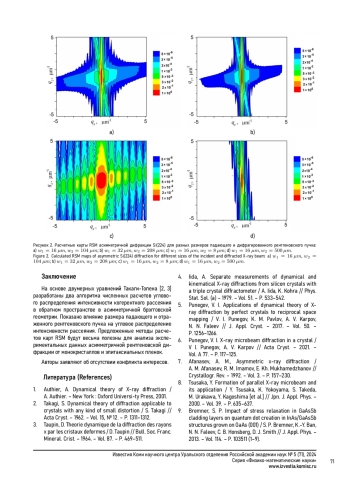
Теоретически исследована асимметричная динамическая дифракция ограниченных рентгеновских пучков в кристаллах с применением уравнений Такаги-Топена, включая численное решение с использованием узловой сетки и вычисления рентгеновских полей в Фурье пространстве. Выполнено моделирование карт распределения интенсивности рассеяния от кристалла кремния вблизи узла обратной решетки в зависимости от размеров рентгеновских пучков.
Идентификаторы и классификаторы
Обычно при рассмотрении динамической теории дифракции в идеальном кристалле предполагается, что на поверхность образца падает неограниченная плоская рентгеновская волна [1]. Такая модель удобна, поскольку в уравнениях Такаги–Топена [2, 3], записанных в прямоугольной системе координат, сразу отбрасывается производная вдоль латерального направления, при этом дифракционная задача становится одномерной.
Список литературы
1. Authier, A. Dynamical theory of X-ray diffraction / A. Authier. - New York: Oxford Universi-ty Press, 2001.
2. Takagi, S. Dynamical theory of diffraction applicable to crystals with any kind of small distortion / S. Takagi // Acta Cryst. - 1962. - Vol. 15, № 12. - P. 1311-1312.
3. Taupin, D. Theorie dynamique de la diffraction des rayons x par les cristaux deformes / D. Taupin // Bull. Soc. Franc. Mineral. Crist. - 1964. - Vol. 87. - P. 469-511.
4. Iida, A. Separate measurements of dynamical and kinematical X-ray diffractions from silicon crystals with a triple crystal diffractometer / A. Iida, K. Kohra // Phys. Stat. Sol. (a) - 1979. - Vol. 51. - P. 533-542.
5. Punegov, V. I. Applications of dynamical theory of Xray diffraction by perfect crystals to reciprocal space mapping / V. I. Punegov, K. M. Pavlov, A. V. Karpov, N. N. Faleev // J. Appl. Cryst. - 2017. - Vol. 50. - P. 1256-1266. EDN: XODGAF
6. Punegov, V. I. X-ray microbeam diffraction in a crystal / V I. Punegov, A. V. Karpov // Acta Cryst. - 2021. - Vol. A 77. - P. 117-125.
7. Afanasev, A. M., Asymmetric x-ray diffraction / A. M. Afanasev, R. M. Imamov, E. Kh. Mukhamedzhanov // Crystallogr. Rev. - 1992. - Vol. 3. - P. 157-230. EDN: XOCJIJ
8. Tsusaka, Y. Formation of parallel X-ray microbeam and its application / Y. Tsusaka, K. Yokoyama, S. Takeda, M. Urakawa, Y. Kagoshima [et al.] // Jpn. J. Appl. Phys. - 2000. - Vol. 39. - P. 635-637.
9. Bremner, S. P. Impact of stress relaxation in GaAsSb cladding layers on quantum dot creation in InAs/GaAsSb structures grown on GaAs (001) / S. P. Bremner, K.-Y. Ban, N. N. Faleev, C. B. Honsberg, D. J. Smith // J. Appl. Phys. - 2013. - Vol. 114. - P. 103511 (1-9). EDN: ROSGNL
Выпуск
Другие статьи выпуска
Авторы показывают, что модель Леонтьева линейного многоотраслевого баланса можно получить предельным переходом по некоторым параметрам из линейной модели обмена с изменением экономического статуса некоторых участников хозяйственного процесса. Более того, саму модель Леонтьева можно подвергнуть такой же предельной процедуре и получить новую модель Леонтьева. Параметры могут иметь разные интерпретации, зависящие от конкретной ситуации в экономике: смена приоритетов в народном хозяйстве и др.
Работа посвящена исследованию связи численной дис- персии, возникающей при FDTD-моделировании распро- странения электромагнитных сигналов в недиспергиру- ющих однородных средах, оптически отличных от ваку- ума, с числом Куранта в 2D-случае. Основные результа- ты сформулированы в форме четырех утверждений, а так- же ряда следствий и замечаний, определяющих харак- тер численной дисперсии, оптимальное значение числа Куранта и границы применимости метода. Доказано, что оптимальный выбор числа Куранта устраняет численную дисперсию и расширяет возможности разработанного чис- ленного алгоритма на среды, оптически менее плотные, чем вакуум, а также левые среды.
Теоретически рассмотрена рентгеновская Лауэ дифракция в кристалле кремния с термомиграционными каналами Si(Al). На основе модели упругих полей атомных смещений в канале получены выражения распределения деформаций для описания дифракции в геометрии Лауэ. Выполнен численный расчет распределения интенсивности рентгеновского рассеяния вблизи узла обратной решетки. Показано отличие дифракции в совершенном и деформированном кристалле.
Геометрия Лобачевского моделирует среду с материальными уравнениями специального вида: Di = ϵ0ϵikEk, Bi = μ0μikHk, где два тензора совпадают: ϵik(x) = μik(x). В пространстве Лобачевского используются квазидекартовые координаты (x, y, z), они моделируют среду, неоднородную вдоль оси z. В этих координатах построены точные решения уравнений Максвелла в комплексной форме Майораны-Оппенгеймера. Задача сводится к дифференциальному уравнению второго порядка для некоторой основной функции, это уравнение может быть связано с одномерной задачей Шредингера для частицы во внешнем потенциальном поле U(z) = U0e2z. В квантовой механике геометрия Лобачевского действует как эффективный потенциальный барьер с коэффициентом отражения R = 1; в электродинамическом контексте эта геометрия действует как распределенное в пространстве идеальное зеркало. Проникновение электромагнитного поля в эффективную среду вдоль оси z зависит от характеристик электромагнитной волны ω, k2 1 +k2 2 и радиуса кривизны ρ пространства Лобачевского. Построенные обобщенные волновые решения f(t, x, y, z) = E + iB и соответствующая система уравнений преобразуются в действительную форму, что позволяет связать геометрические характеристики с выражениями для эффективных тензоров электрической и магнитной проницаемостей.
Цель работы - исследование нерелятивистского приближения в 39-компонентной теории частицы со спином 2. Используется явный вид матриц Γa размерности 39×39 основного уравнения, записанного в декартовых координатах и с учетом внешних электромагнитных полей. Для выделения в волновой функции больших и малых переменных с точки зрения нерелятивистского приближения используются проективные операторы, строящиеся на основе минимального полинома 7-й степени для матрицы Γ0. Разбиение на большие и малые переменные проведено в явном виде, в каждой группе найдены независимые переменные, остальные выражены через них. В частности, среди больших переменных независимыми являются только 5. Выведено нерелятивистское уравнение для 5-компонентной волновой функции; в нем выделен член, описывающий взаимодействие магнитного момента частицы с внешним магнитным полем. Этот дополнительный член взаимодействия строится из проекций оператора спина и компонент внешнего магнитного поля.
В настоящей работе система 11 уравнений для массивной частицы Штюкельберга исследуется в присутствии внешнего однородного электрического поля. Применяет- ся тетрадный формализм, согласно методу Тетрода-Вейля-Фока-Иваненко. Используются цилиндрические координаты и соответствующая диагональная тетрада. Разделив переменные, получили систему дифференциальных уравнений первого порядка в частных производных по координатам (r, z). Для решения этой системы применяется метод Федорова-Гронского, согласно которому на основе 11-мерного оператора спина введены три проективных оператора, позволяющие разложить полную волновую функцию в сумму трех частей. Согласно общему методу, зависимость каждой проективной составляющей от переменной r должна определяться только одной функцией. Также используются дифференциальные ограничения первого порядка, совместимые с системой уравнений и позволяющие преобразовать все уравнения в частных производных по координатам (r, z) в обыкновенные дифференциальные уравнения по переменной z. Последняя система решена в терминах вырожденных гипергеометрических функций. Построены четыре независимые решения, в отличие от случая обычной частицы со спином 1, описываемой уравнением Даффина-Кемера, когда возможны только три решения.
Изучены контракции калибровочных моделей с ортогональными группами Кэли-Клейна SO(2; ϵ), SO(3; ϵ) и унитарными группами SU(2; ϵ) в качестве калибровочных групп. В пределе нулевых контракционных параметров ортогональные группы изоморфны неполупростым группам Евклида и Ньютона соответствующей размерности, а пространства полей материи становятся расслоенными пространствами с вырожденной метрикой. Особое внимание уделено согласованию спонтанного нарушения симметрии с процедурой контракции групп. Показано, что контрактированные калибровочные теории описывают тот же набор полей с теми же массами, что и теории с исходными простыми группами, если выбранный вакуум в соответствующем пределе принадлежал базе расслоенного пространства полей материи. Получены зависящие от контракционных параметров лагранжианы моде- лей, что позволяет проследить порядок обнуления слагаемых в лагранжианах при стремлении параметров контракции к нулю.
В работе рассматривается круговая арка, нагруженная равномерно распределенным нормальным давлением, направленным к центру. Концы арки прикреплены тросами, один конец которых прикреплен к дуге арки под соответствующим углом, и расстояние между точками прикрепления тросов не может увеличиваться. Определены значения давления, при которых возможны искривленные формы равновесия арки, и найдено наименьшее из этих значений, являющееся критической силой.
Фигурой постоянной ширины называется такая фигура, у которой расстояние между любыми параллельными опорными прямыми одно и то же. Ясно, что таким свойством обладает круг, но не только. Простешей фигурой постоянной ширины (кроме круга) является треугольник Рёло. В настоящей работе решается задача устойчивости треугольника Рёло, находящегося под действием нормальной нагрузки. Получено значение критического давления.
Перманент многомерных матриц выражен в терминах операций над элементами коммутативной алгебры с нильпотентными индекса 2 образующими. С помощью техники, основанной на данной взаимосвязи, доказано несколько свойств перманента. Изучены различные виды многомерных перестановок. Перманент многомерных матриц рассмотрен с точки зрения перечисляющей функции многомерных перестановок.
Показано, что стандартная конструкция уравнений Лакса на алгебрах Ли может быть распространена на супералгебры Ли, в которых четное подпространство несет в себе обычные уравнения Лакса. Расширенные уравнения наследуют существование канонических следовых полиномиальных интегралов движения. В нечетном подпространстве существует дополнительный набор интегралов с нетривиальной гомологической структурой пространства орбит. Это устанавливает любопытную алгебраическую связь между интегрируемыми эволюционными уравнениями, суперсимметрией и теорией деформаций.
Статистика статьи
Статистика просмотров за 2025 год.
Издательство
- Издательство
- ФИЦ КОМИ НЦ УРО РАН
- Регион
- Россия, Сыктывкар
- Почтовый адрес
- Коммунистическая ул., 24
- Юр. адрес
- 167000, Респ Коми, г Сыктывкар, ул Коммунистическая, д 24
- ФИО
- Дёгтева Светлана Владимировна (ДИРЕКТОР)
- E-mail адрес
- bergman@frc.komisc.ru
- Контактный телефон
- +7 (821) 2245398
- Сайт
- http:/nb.komisc.ru