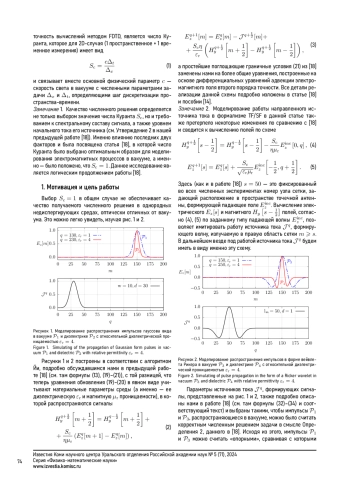
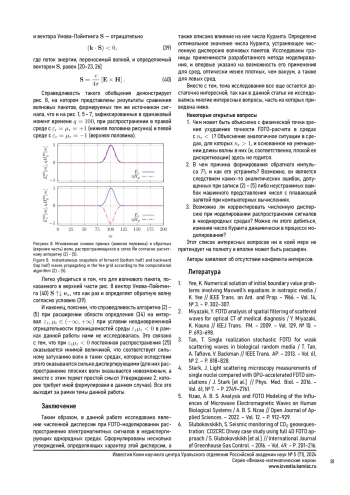
Работа посвящена исследованию связи численной дис- персии, возникающей при FDTD-моделировании распро- странения электромагнитных сигналов в недиспергиру- ющих однородных средах, оптически отличных от ваку- ума, с числом Куранта в 2D-случае. Основные результа- ты сформулированы в форме четырех утверждений, а так- же ряда следствий и замечаний, определяющих харак- тер численной дисперсии, оптимальное значение числа Куранта и границы применимости метода. Доказано, что оптимальный выбор числа Куранта устраняет численную дисперсию и расширяет возможности разработанного чис- ленного алгоритма на среды, оптически менее плотные, чем вакуум, а также левые среды.
Идентификаторы и классификаторы
Численные методы решения волновых уравнений играют важную роль не только в конкретных технических приложениях, но и в фундаментальной науке в целом. К таким методам относится и FDTD (Finite-Difference TimeDomain) [1], некоторые особенности которого и являются предметом данной работы.
Список литературы
1. Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media / K. Yee // IEEE Trans. on Ant. and Prop. - 1966. - Vol. 14, № 3. - P. 302-307.
2. Miyazaki, Y. FDTD analysis of spatial filtering of scattered waves for optical CT of medical diagnosis / Y. Miyazaki, K. Kouno // IEEJ Trans. FM. - 2009. - Vol. 129, № 10. - P. 693-698.
3. Tan, T. Single realization stochastic FDTD for weak scattering waves in biological random media / T. Tan, A. Taflove, V. Backman // IEEE Trans. AP. - 2013. - Vol. 61, № 2. - P. 818-828.
4. Stark, J. Light scattering microscopy measurements of single nuclei compared with GPU-accelerated FDTD simulations / J. Stark [et al.] // Phys. Med. Biol. - 2016. - Vol. 61, № 7. - P. 2749-2761. EDN: WOXJAV
5. Nzao, A. B. S. Analysis and FDTD Modeling of the Influences of Microwave Electromagnetic Waves on Human Biological Systems / A. B. S. Nzao // Open Journal of Applied Sciences. - 2022. - Vol. 12. - P. 912-929. EDN: ZJTJYI
6. Glubokovskikh, S. Seismic monitoring of CO2 geosequestration: CO2CRC Otway case study using full 4D FDTD approach / S. Glubokovskikh [et al.] // International Journal of Greenhouse Gas Control. - 2016. - Vol. 49. - P. 201-216. EDN: WVUGPZ
7. Yu, J. Modeling of Whole-Space Transient Electromagnetic Responses Based on FDTD and its Application in the Mining Industry / J. Yu, R. Malekian, J. Chang, B. Su // IEEE Trans. Indust. Inform. - 2017. - Vol. 13, № 6. - P. 2974-2982.
8. Fantoni, A. A model for the refractive index of amorphous silicon for FDTD simulation of photonics waveguides / A. Fantoni, P. Loureniço, M. Vieira // International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Copenhagen, Denmark. - 2017. - P. 167-168.
9. Mishra, C. S. FDTD approach to photonic based angular waveguide for wide range of sensing application / C. S. Mishra [et al.] // Optik. - 2019. - Vol. 176. - P. 56-59.
10. Mohanty, S. P. FDTD method to photonic waveguides for application of optical demultiplexer at 3-communication windows / S. P. Mohanty, S. K. Sahoo, A. Panda, G. Palai // Optik. - 2019. - Vol. 185. - P. 146-150.
11. Bakirtzis, S. FDTD-Based Diffuse Scattering and Transmission Models for Ray Tracing of Millimeter-Wave Communication Systems / S. Bakirtzis, T. Hashimoto, C. D. Sarris // IEEE Trans. AP. - 2021. - Vol. 69, № 6. - P. 3389-3398.
12. Makarov, P. Simulation of Electromagnetic Wave Propagation in Magnetic Randomly Inhomogeneous Magnetic Media / P. Makarov [et al.] // IEEE Magnetics Letters. - 2022. - Vol. 13. - P. 1-5. EDN: IDFKBY
13. Макаров, П. А. Моделирование распространения электромагнитных волн в магнитно-неоднородных средах / П. А. Макаров, В. А. Устюгов, В. И. Щеглов // Известия Коми научного центра Уральского отделения Российской академии наук. Серия “Физико-математические науки”. - 2022. - № 5 (57). - C. 100-105.
14. Schneider, J. B. Understanding the Finite-Difference Time-Domain Method / J. B. Schneider. - www.eecs.wsu.edu/~schneidj/ufdtd, 2010. - 403 p.
15. Inan, U. S. Numerical electromagnetics. The FDTD method / U. S. Inan, R. A. Marshall. - Cambridge: Cambridge University Press, 2011. - 406 p.
16. Taflove, A. Advances in FDTD computational electrodynamics photonics and nanotechnology / A. Taflove, A. Oskooi, S. G. Johnson. - Boston: Artech House, 2013. - 639 p.
17. Langtangen, H. P. Finite Difference Computing with PDEs: A Modern Software Approach / H. P. Langtangen, S. Linge. - Springer Cham, 2017. - XXIII. - 507 p.
18. Макаров, П. А. Особенности численного моделирования уравнений Максвелла методом FDTD в однородной и неоднородной формулировках / П. А. Макаров, В. А. Устюгов, В. И. Щеглов // Известия Коми научного центра Уральского отделения Российской академии наук. Серия “Физико-математические науки”. - 2023. - № 4 (62). - C. 96-107.
19. Виноградова, М. Б. Теория волн / М. Б. Виноградова, О. В. Руденко, А. П. Сухоруков. - Москва: Наука, 1979. - 384 с.
20. Бредов, М. М. Классическая электродинамика / М. М. Бредов, В. В. Румянцев, И. Н. Топтыгин. - Москва: Наука, 1985. - 400 с.
21. Кугушев, А. М. Основы радиоэлектроники. Электродинамика и распространение радиоволн / А. М. Кугушев, Н. С. Голубева, В. Н. Митрохин. - Москва: Изд-во МГТУ им. Н. Э. Баумана, 2001. - 368 с.
22. Шустер, А. Введение в теоретическую оптику / А. Шустер. - Ленинград, Москва: ОНТИ, гл. ред. общетех. лит., 1935. - 376 с.
23. Веселаго, В. Г. Электродинамика веществ с одновременно отрицательными значениями ε и μ / В. Г. Веселаго // УФН. - 1967. - T. 92, № 3. - C. 517-526.
24. Pendry, J. Negative refraction / J. Pendry // Contemporary Physics - 2004. - V. 45, № 3. - C. 191-202. EDN: WNROPD
25. Агранович, В. М. Пространственная дисперсия и отрицательное преломление света / В. М. Агранович, Ю. Н. Гартштейн // УФН - 2006. - T. 176, № 10. - C. 1052-1068. EDN: HVGXEN
26. Ландсберг, Г. С. Оптика / Г. С. Ландсберг. - Москва: ФИЗМАТЛИТ, 2010. - 848 с. EDN: RBBFMD
27. Коткин, Г. Л. Лекции по аналитической механике / Г. Л. Коткин, В. Г. Сербо, А. И. Черных. - Москва, Ижевск: НИЦ РХД, 2017. - 236 с.
28. Карлов, Н. В. Колебания, волны, структуры / Н. В. Карлов, Н. А. Кириченко. - Москва: Физматлит, 2008. - 498 с. EDN: SUQCNZ
29. Флюгге, З. Задачи по квантовой механике, Т. I / З. Флюгге. - Москва: Мир, 1974. - 342 с.
30. Шевченко, В. В. Прямые и обратные волны: три определения, их взаимосвязь и условия применимости / В. В. Шевченко // УФН. - 2007. - T. 177, № 3. - C. 301-306. EDN: HYRLJB
Выпуск
Другие статьи выпуска
Авторы показывают, что модель Леонтьева линейного многоотраслевого баланса можно получить предельным переходом по некоторым параметрам из линейной модели обмена с изменением экономического статуса некоторых участников хозяйственного процесса. Более того, саму модель Леонтьева можно подвергнуть такой же предельной процедуре и получить новую модель Леонтьева. Параметры могут иметь разные интерпретации, зависящие от конкретной ситуации в экономике: смена приоритетов в народном хозяйстве и др.
Теоретически исследована асимметричная динамическая дифракция ограниченных рентгеновских пучков в кристаллах с применением уравнений Такаги-Топена, включая численное решение с использованием узловой сетки и вычисления рентгеновских полей в Фурье пространстве. Выполнено моделирование карт распределения интенсивности рассеяния от кристалла кремния вблизи узла обратной решетки в зависимости от размеров рентгеновских пучков.
Теоретически рассмотрена рентгеновская Лауэ дифракция в кристалле кремния с термомиграционными каналами Si(Al). На основе модели упругих полей атомных смещений в канале получены выражения распределения деформаций для описания дифракции в геометрии Лауэ. Выполнен численный расчет распределения интенсивности рентгеновского рассеяния вблизи узла обратной решетки. Показано отличие дифракции в совершенном и деформированном кристалле.
Геометрия Лобачевского моделирует среду с материальными уравнениями специального вида: Di = ϵ0ϵikEk, Bi = μ0μikHk, где два тензора совпадают: ϵik(x) = μik(x). В пространстве Лобачевского используются квазидекартовые координаты (x, y, z), они моделируют среду, неоднородную вдоль оси z. В этих координатах построены точные решения уравнений Максвелла в комплексной форме Майораны-Оппенгеймера. Задача сводится к дифференциальному уравнению второго порядка для некоторой основной функции, это уравнение может быть связано с одномерной задачей Шредингера для частицы во внешнем потенциальном поле U(z) = U0e2z. В квантовой механике геометрия Лобачевского действует как эффективный потенциальный барьер с коэффициентом отражения R = 1; в электродинамическом контексте эта геометрия действует как распределенное в пространстве идеальное зеркало. Проникновение электромагнитного поля в эффективную среду вдоль оси z зависит от характеристик электромагнитной волны ω, k2 1 +k2 2 и радиуса кривизны ρ пространства Лобачевского. Построенные обобщенные волновые решения f(t, x, y, z) = E + iB и соответствующая система уравнений преобразуются в действительную форму, что позволяет связать геометрические характеристики с выражениями для эффективных тензоров электрической и магнитной проницаемостей.
Цель работы - исследование нерелятивистского приближения в 39-компонентной теории частицы со спином 2. Используется явный вид матриц Γa размерности 39×39 основного уравнения, записанного в декартовых координатах и с учетом внешних электромагнитных полей. Для выделения в волновой функции больших и малых переменных с точки зрения нерелятивистского приближения используются проективные операторы, строящиеся на основе минимального полинома 7-й степени для матрицы Γ0. Разбиение на большие и малые переменные проведено в явном виде, в каждой группе найдены независимые переменные, остальные выражены через них. В частности, среди больших переменных независимыми являются только 5. Выведено нерелятивистское уравнение для 5-компонентной волновой функции; в нем выделен член, описывающий взаимодействие магнитного момента частицы с внешним магнитным полем. Этот дополнительный член взаимодействия строится из проекций оператора спина и компонент внешнего магнитного поля.
В настоящей работе система 11 уравнений для массивной частицы Штюкельберга исследуется в присутствии внешнего однородного электрического поля. Применяет- ся тетрадный формализм, согласно методу Тетрода-Вейля-Фока-Иваненко. Используются цилиндрические координаты и соответствующая диагональная тетрада. Разделив переменные, получили систему дифференциальных уравнений первого порядка в частных производных по координатам (r, z). Для решения этой системы применяется метод Федорова-Гронского, согласно которому на основе 11-мерного оператора спина введены три проективных оператора, позволяющие разложить полную волновую функцию в сумму трех частей. Согласно общему методу, зависимость каждой проективной составляющей от переменной r должна определяться только одной функцией. Также используются дифференциальные ограничения первого порядка, совместимые с системой уравнений и позволяющие преобразовать все уравнения в частных производных по координатам (r, z) в обыкновенные дифференциальные уравнения по переменной z. Последняя система решена в терминах вырожденных гипергеометрических функций. Построены четыре независимые решения, в отличие от случая обычной частицы со спином 1, описываемой уравнением Даффина-Кемера, когда возможны только три решения.
Изучены контракции калибровочных моделей с ортогональными группами Кэли-Клейна SO(2; ϵ), SO(3; ϵ) и унитарными группами SU(2; ϵ) в качестве калибровочных групп. В пределе нулевых контракционных параметров ортогональные группы изоморфны неполупростым группам Евклида и Ньютона соответствующей размерности, а пространства полей материи становятся расслоенными пространствами с вырожденной метрикой. Особое внимание уделено согласованию спонтанного нарушения симметрии с процедурой контракции групп. Показано, что контрактированные калибровочные теории описывают тот же набор полей с теми же массами, что и теории с исходными простыми группами, если выбранный вакуум в соответствующем пределе принадлежал базе расслоенного пространства полей материи. Получены зависящие от контракционных параметров лагранжианы моде- лей, что позволяет проследить порядок обнуления слагаемых в лагранжианах при стремлении параметров контракции к нулю.
В работе рассматривается круговая арка, нагруженная равномерно распределенным нормальным давлением, направленным к центру. Концы арки прикреплены тросами, один конец которых прикреплен к дуге арки под соответствующим углом, и расстояние между точками прикрепления тросов не может увеличиваться. Определены значения давления, при которых возможны искривленные формы равновесия арки, и найдено наименьшее из этих значений, являющееся критической силой.
Фигурой постоянной ширины называется такая фигура, у которой расстояние между любыми параллельными опорными прямыми одно и то же. Ясно, что таким свойством обладает круг, но не только. Простешей фигурой постоянной ширины (кроме круга) является треугольник Рёло. В настоящей работе решается задача устойчивости треугольника Рёло, находящегося под действием нормальной нагрузки. Получено значение критического давления.
Перманент многомерных матриц выражен в терминах операций над элементами коммутативной алгебры с нильпотентными индекса 2 образующими. С помощью техники, основанной на данной взаимосвязи, доказано несколько свойств перманента. Изучены различные виды многомерных перестановок. Перманент многомерных матриц рассмотрен с точки зрения перечисляющей функции многомерных перестановок.
Показано, что стандартная конструкция уравнений Лакса на алгебрах Ли может быть распространена на супералгебры Ли, в которых четное подпространство несет в себе обычные уравнения Лакса. Расширенные уравнения наследуют существование канонических следовых полиномиальных интегралов движения. В нечетном подпространстве существует дополнительный набор интегралов с нетривиальной гомологической структурой пространства орбит. Это устанавливает любопытную алгебраическую связь между интегрируемыми эволюционными уравнениями, суперсимметрией и теорией деформаций.
Статистика статьи
Статистика просмотров за 2025 год.
Издательство
- Издательство
- ФИЦ КОМИ НЦ УРО РАН
- Регион
- Россия, Сыктывкар
- Почтовый адрес
- Коммунистическая ул., 24
- Юр. адрес
- 167000, Респ Коми, г Сыктывкар, ул Коммунистическая, д 24
- ФИО
- Дёгтева Светлана Владимировна (ДИРЕКТОР)
- E-mail адрес
- bergman@frc.komisc.ru
- Контактный телефон
- +7 (821) 2245398
- Сайт
- http:/nb.komisc.ru