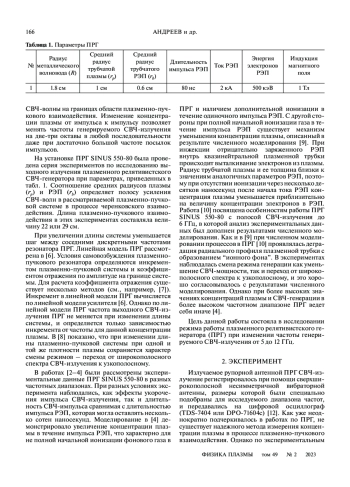
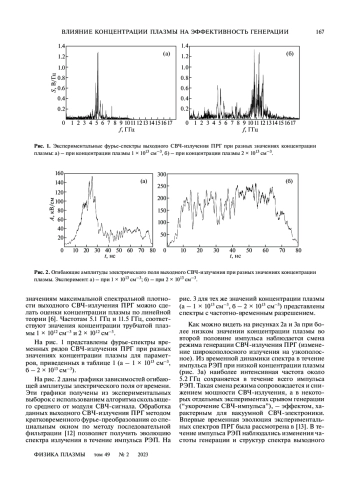
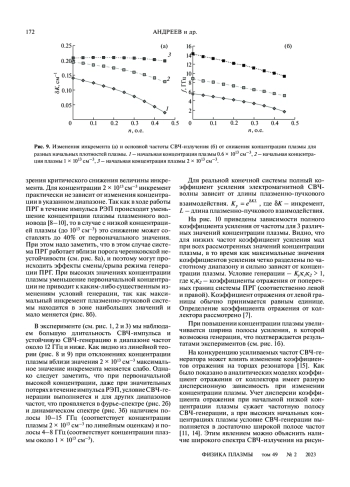
Рассмотрены особенности экспериментальной работы плазменного релятивистского СВЧ-генератора (ПРГ) Sinus 550-80 при разных значениях концентрации плазмы. Рассмотрены два значения концентрации плазмы, при которых центральные частоты выходного СВЧ-излучения ПРГ были равны 5.1 ГГц и 11.5 ГГц. Численное моделирование демонстрирует снижение концентрации электронов плазмы в результате действия заряда релятивистского электронного пучка (РЭП) при черенковском взаимодействии и возникновение “ионного фона” в течение импульса ПРГ. При низких концентрациях плазмы это может приводить к изменению условий СВЧ-генерации – сопровождаться не только изменением широкополосного излучения на узкополосное, но и снижением мощности излучения. В то же время при больших значениях концентрации плазмы при генерации СВЧ-излучении на высоких частотах средняя амплитуда электрического поля волны практически не меняется в течение импульса РЭП, а излучение остается широкополосным. Анализ результатов экспериментов и численного моделирования подкреплен оценками линейной теории, доказывающей, что при более высоких значениях концентрации плазмы ПРГ работает более устойчиво.
Предпросмотр статьи
